K Means Clustering

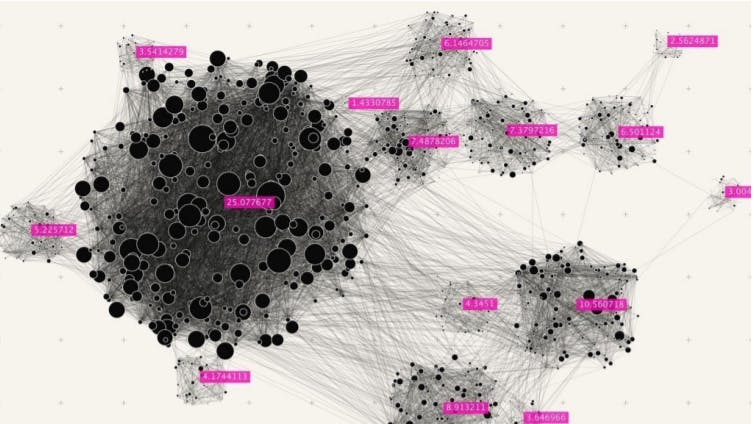
Framework of unsupervised learning

Given : Pairs (x1; y1),......,(xn; yn). Think of x as input and y as output.

Learn : A function f (x) that accurately predicts yi ≈ f (xi) on this data.

Goal : Use the function f (x) to predict new y0 given x0.

K-means algorithm

1. k random points of the data set are chosen to be centroids.
2. Distances between every data point and the k centroids are calculated and stored.
3. Based on distance calculates, each point is assigned to the nearest cluster
4. New cluster centroid positions are updated: similar to finding a mean in the point locations
5. If the centroid locations changed, the process repeats from step 2, until the calculated new center stays the same, which signals that the clusters' members and centroids are now set.

The objective function for the K-means clustering algorithm is the squared error function:

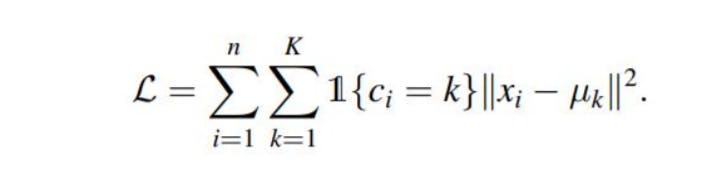
Where, ||xi - uk||^2 is the Euclidean distance between a point, xi and a centroid uk.

Optimization

Here we have to consider two parameters for minimizing the objective function (ci, uk). But we calculate the gradient of only one parameter at a time for performing the gradient descent method. Due to this here we introduce another method for optimizing the loss function called Co-ordinate Descent.

Coordinate Descent

Updating C

Given µ = (µ1,....,µK), update c = (c1,........,cn).

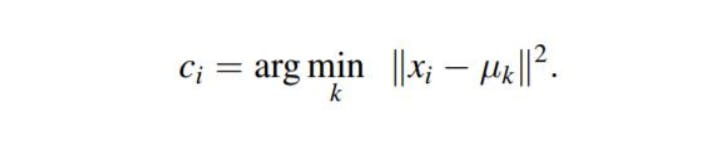
Derivation

Pseudocode

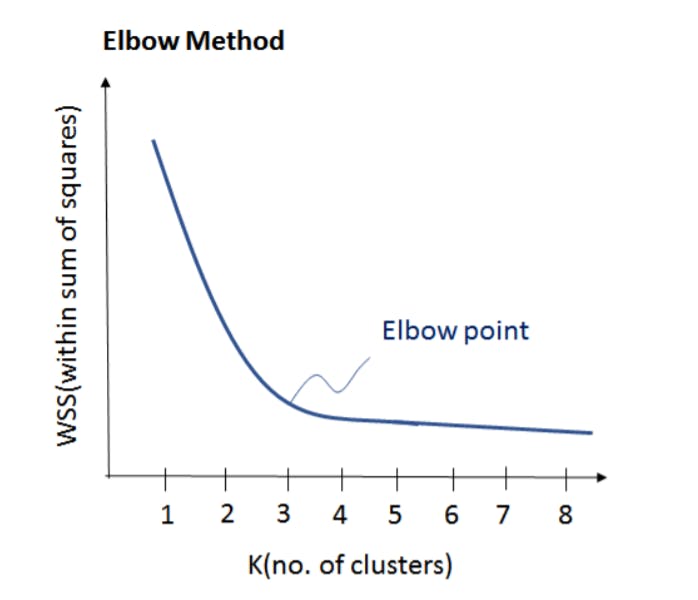
After understanding the entire algorithm you would have gotten an obvious question in mind, How many clusters we should form? Here is the answer to your question

Number of Cluster K

Elbow Method

Code Implementation

def calc_distance(X1, X2):
    return (sum((X1 - X2)**2))**0.5

# Assign cluster clusters based on closest centroid

def assign_clusters(centroids, cluster_array):
    clusters = []

    for i in range(cluster_array.shape[0]):
        distances = []
        for centroid in centroids:
            distances.append(calc_distance(centroid,cluster_array[i]))
        cluster = [z for z, val in enumerate(distances) if val==min(distances)]
        clusters.append(cluster[0])
    return clusters

# Calculate new centroids based on each cluster's mean

def calc_centroids(clusters, cluster_array):
    new_centroids = []
    cluster_df = pd.concat([pd.DataFrame(cluster_array),pd.DataFrame(clusters,columns=['cluster'])],axis=1)
    for c in set(cluster_df['cluster']):
        current_cluster = cluster_df[cluster_df['cluster']\==c][cluster_df.columns[:-1]]
        cluster_mean = current_cluster.mean(axis=0)
        new_centroids.append(cluster_mean)
    return new_centroids

# Calculate variance within each cluster

def calc_centroid_variance(clusters, cluster_array):
    sum_squares = []
    cluster_df = pd.concat([pd.DataFrame(cluster_array),
    pd.DataFrame(clusters,columns=['cluster'])],axis=1)
    for c in set(cluster_df['cluster']):
        current_cluster = cluster_df[cluster_df['cluster']\==c][cluster_df.columns[:-1]]
        cluster_mean = current_cluster.mean(axis=0)
        mean_repmat = np.matlib.repmat(cluster_mean,
        current_cluster.shape[0],1)
        sum_squares.append(np.sum(np.sum((current_cluster - mean_repmat)**2)))
    return sum_squares

k = 4
cluster_vars = []
centroids = [cluster_array[i+2] for i in range(k)]
clusters = assign_clusters(centroids, cluster_array)
initial_clusters = clusters
print(0, round(np.mean(calc_centroid_variance(clusters, cluster_array))))
for i in range(20):
    centroids = calc_centroids(clusters, cluster_array)
    clusters = assign_clusters(centroids, cluster_array)
    cluster_var = np.mean(calc_centroid_variance(clusters,cluster_array))
    cluster_vars.append(cluster_var)
    print(i+1, round(cluster_var))